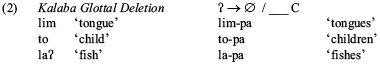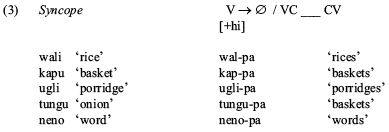Re-reading just the opening few pages of Odden’s “Ordering” paper (bits of which were originally discussed here) reveals at least two more mischaracterizations of both Optimality Theory and rule-ordering theory. These mischaracterizations would just be funny if it weren’t for the fact that they are being perpetrated by a phonologist who has arguably made a career out of poking holes in theories (or socks). The fact that I have to waste my time (and yours, if you continue reading this) poking holes in the hole-poking is just plain sad.
1. Partial ordering and n!
On p. 2 of the paper, Odden wonders whether the elimination of derivational steps results in “some kind of simplification of grammars”. The discussion that follows clarifies the fact that Odden means “some kind of reduction in the number of possible grammars”:
Allowing rules to be explicitly ordered, under the standard theory of linear rule ordering, allows a given set of n rules to be mapped onto n! grammars (thus 5 rules maps onto 120 grammars and 8 rules maps onto 40,320 grammars).
This quotation is followed by the first footnote of the paper:
In OT, constraints are not strictly ranked and are only partially ordered. With partial ordering (ranking), 5 constraints can be ranked 4,231 ways and 8 constraint [sic] can be ranked 431,723,379 ways. The general function for computing the number of partial orderings is not known, and values are only known up to n=14 (98,484,324,257,128,207,032,183).
Wow, them are some big numbers. But Odden is seriously mischaracterizing both rule-ordering theory and Optimality Theory here, because he appears to misunderstand what a partial ordering means in both theories. Let’s clarify:
| (i) | A grammar is not (always) a unique ordering of rules / constraints. |
| Two rules / constraints that do not directly interact typically cannot be ordered with respect to each other, except by transitivity. The number of total orderings of 5 rules / constraints is 120, but the number of distinct grammars resulting from these 120 orderings depends on how these rules / constraints interact. | |
| For example, the 120 possible rankings of the 5 constraints in Chapter 6 of Prince & Smolensky 1993 result in only 9 distinct grammars. This is a toy example but it proves the point. I’m sure a perfectly parallel example can be drawn from the rule-ordering literature. | |
| (ii) | Partial orderings are not crucial. |
| In standard approaches to both rule-ordering theory and OT, orderings are typically only partial because there is often no evidence available, direct or otherwise, for the relative ordering of some of the rules / constraints in a given analysis. Since these nonorderings are not crucial, the relevant rules / constraints can be ordered either way with no effect on the predicted set of outputs. The resulting number of predicted grammars is thus less than n!, not more. | |
| Some versions of the idea of “tied constraints” do amount to crucial nonranking, a possibility explicitly discussed and rejected by Prince & Smolensky 1993, p. 55 fn. 31. (Various ways to construe the idea of tied constraints are thoroughly discussed by Müller (1999).) Crucial nonordering of rules has probably also been explicitly discussed and has possibly also been rejected somewhere in the rule-ordering literature, but it is likewise not ruled out in principle so both frameworks are in the same boat in this case. |
But perhaps it’s unfair to criticize Odden for not understanding the relationship between partial ordering and factorial typology. Even though the concepts apply in pretty much the same way to both rule ordering and constraint ranking, they were not so central to theoretical discussions surrounding rule ordering. The usual claims of constraint universality in OT are what brought these concepts to the fore; since Odden doesn’t do OT, maybe it’s understandable for him to mischaracterize the concepts.
2. Son of “you can’t do that with rules”
Beginning on p. 3, Odden discusses another hypothetical situation (before the one I’ve already commented on here) that he claims is possible to describe with OT + Sympathy Theory but not with rule-ordering theory.
Under standard linear ordering, if rule A precedes B and B precedes C, then A precedes C (and therefore C does not precede A). Common-sensical as this may be, this is an empirically testable hypothesis, and it is possible to construct hypothetical languages which require such a prohibited interaction. The imaginary language Kalaba cannot be modeled in derivational theory, since it involves exactly this contradiction. First, the language has a rule (2), deleteing glottal stop before another consonant, which we see applying before the plural suffix pa.
Second, there is a syncope rule shown in (3) deleting high vowels in a doubly open syllable.
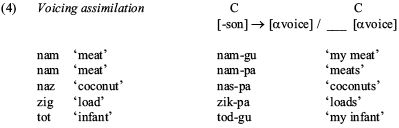
Finally, in (4) there is regressive voicing assimilation that affects obstruents.
The pairwise ordering of these rules is shown in (5). First, Glottal Deletion must precede Syncope. Glottal Deletion in the second form on the right makes the first syllable open, which then allows Syncope to apply to the vowel i in ‘fishes’. Second, Syncope must feed into Voicing Assimilation, as shown by the second set of data, where deletion of the high vowel allows p to assimilate to g in the first example, and allows z to assimilate to p in the second example. Thus we deduce the orderings ‘A precedes B’ and ‘B precedes C’, which in standard derivational theory entails that A precedes C.
The third set of examples in (6) show that, nevertheless, Voicing Assimilation precedes and is counterfed by Glottal Deletion, that is, C must precede A. These examples show that Voicing Assimilation does not take place between obstruents if they were underlyingly separated by a glottal stop, meaning that glottal deletion has not taken place at the stage where Voicing Assimilation applies.
Thus, the non-language Kalaba is predicted to be impossible in standard derivational theory.
Odden then goes on to provide hypothetical data showing that the ordering paradox cannot be resolved cyclically, etc. He then shows that OT with Sympathy Theory can describe this pattern, concluding that “Sympathy Theory allows for interactions which cannot be modelled under standard derivational theory” (p. 5).
There is a rather simple way to describe this pattern with ordered rules. The trick is to decompose Voicing Assimilation into two rules. The first one would be the one in (4), but it precedes Glottal Deletion (2) to account for the data in (6). The second one would be as follows, preceding (and counterbleeding) Syncope (3):
Voicing Assimilation 2:
C V C [–son] → [αvoi] / V __ [+high] [αvoi] V
Of course, this is a highly objectionable rule for a variety of reasons that one could go on and on about. I’m sure Odden would invoke the “general theory of rule construction” again here, but before you swallow that consider Odden’s own words just a couple pages back in the same paper (p. 2):
Positing a limited derivational aspect to OT does increase the power of OT, but it is unclear whether it amounts to surrendering any fundamental principles of the theory (since it is unclear what principles in OT are truly fundamental versus convenient assumptions).
If the (relevant part of the) so-called “general theory of rule construction” can be shown to be any more a fundamental principle of rule-ordering theory than it is a convenient assumption — compared to whatever it is that Odden is alluding to about OT in this quotation, that is — I’ll eat my hat.